Irrational Numbers Are Not Numbers
Last week, I posted a writeup titled “On Non-Scientific Claims.” I wanted to write a sort of follow-up to that. I had loosely mentioned how irrational numbers were actually not numbers and were just yet another example of dogma. Here, I want to address that directly. What Even Is a Number?
Pi: The Infinite Poster Child
Take pi as an example. It is a non-terminating decimal. Its digits go on forever—it is literally infinite. This alone completely destroys the idea that irrational numbers are as valid as real numbers. Infinity is not scalable. It does not have a fixed quantity. Infinity cannot fit into a box. Infinity does not have a specific, exact place on the number line.
Why the Real Number Line Is a Lie
But the set of real numbers (ℝ) says they do have a place!” The real numbers ℝ include both rational and irrational numbers. In this set, mathematicians insist that irrationals have a precise location. What’s the problem? It’s axiomatic!Axioms: The Silent Dogma of Modern Math
The whole construction rests on assertions that we don’t even know how to fully state without circularity. Worse, these axioms are almost never explicitly justified—they’re just silently assumed. This points to the cancerous way mathematicians have been using axioms (a future writeup on that is coming).Dedekind Cuts vs. the Real Numbers
The crucial thing to note about irrational numbers is that they are convergent infinite processes. They have a starting position but no end. Dedekind cuts are supposed to tell us that if you split the number line into two sets—everything less than the number and everything greater—you can pinpoint the exact location of any real number.The Never-Ending Bisection Paradox
For example, if you want to locate 5.53 on the number line, you throw away everything less than 5 and everything greater than 6, then everything less than 5.5 and greater than 5.6, and you keep refining forever until you supposedly “reach” the exact spot. So what happens when we apply this to something like π = 3.14159…? You start throwing away intervals… and you keep going into the decimals… and any minute now… it never ends! Dun dun dun! Do you see? You are literally splitting the number line infinitely many times. You will never actually reach a final position. This leads to all sorts of weird paradoxes. Dedekind cuts and the standard construction of ℝ constantly contradict each other. While ℝ insists that irrationals exist as completed entities with definite positions, Dedekind cuts indirectly prove that you can never finish the process for an infinite non-repeating decimal. They cannot peacefully coexist in the same room—they’re constantly yelling at each other. Do you understand? Irrational numbers, as usually conceived, do not actually exist.

“But They’re Useful!” – The Weakest Argument in Math “What about utility? Are irrationals considered numbers just because they’re useful?” Sure, they’re useful—but that’s like saying cans are alive because they serve a super-specific purpose. This is the utility argument; never give in to its snares. Sorry, Pythagoras – You Were Right All Along To wrap up, I also want to thank the people who brought light to this idea—mainly rxsapphsire (who goes by Pythagoras on her Discord server). And of course, I owe an apology to the original Pythagoras. You were right all along.
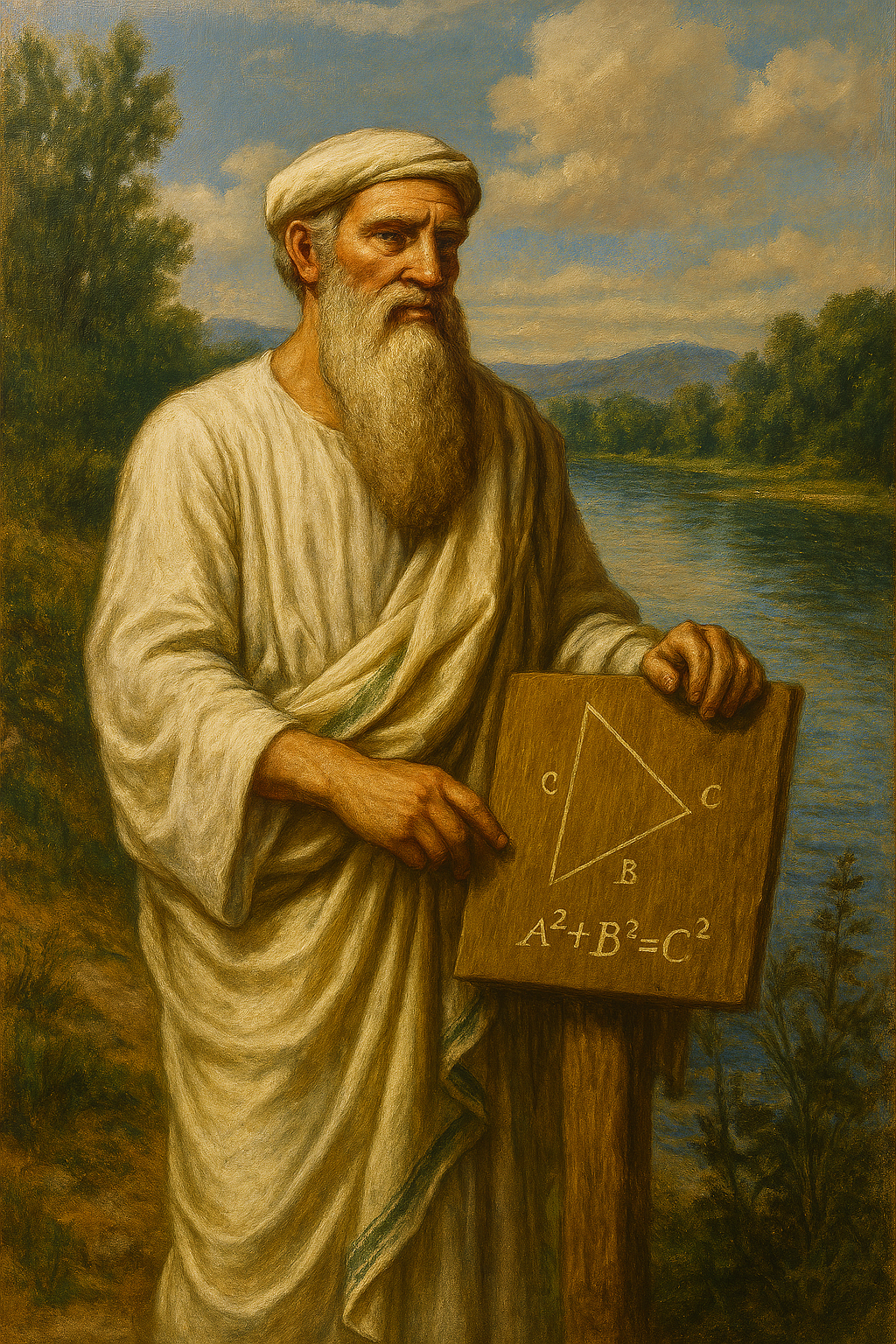




 © 2025 T.E. Havorford (ThomasE.xyz)
© 2025 T.E. Havorford (ThomasE.xyz)